서포트 벡터 머신(Support Vector Machine, SVM)
서포트 벡터 머신은 강력한 학습 알고리즘으로 퍼셉트론의 확장으로 생각할 수 있다.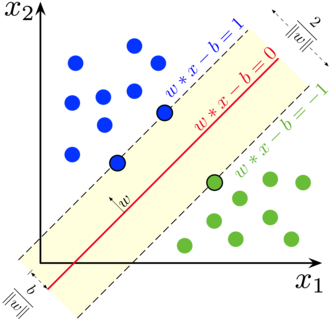
퍼셉트론은 분류 오차를 최소화 했었지만, 서포트 벡터 머신의 최적화 대상은 마진을 최대화 하는 것이다.

마진
마진은 클래스를 구분하는 초평면(결정 경계)과 이 초펴면에 가장 가까운 훈련 샘플 사이의 거리로 정의
이와 같은 샘플들을 서포트 벡터라고 부른다.
큰 마진의 결정 경계를 원하는 이유는 일반화 오차가 낮아지는 경향이 있기 때문이다.
반면 작은 마진의 모델은 과대적합하기 쉽다.
SVM 목적함수는 샘플이 정확하게 분류된다는 제약 조건하에서 2/|w|가 최대화함으로서 마진을 최대화 하는 것이다.


more details
Support Vector Machine(SVM)은 원 훈련(또는 학습) 데이터를 비선형 매핑을 통해 고차원으로 변환한다.
이 새로운 차원에서 초평면(hyperplane)을 최적으로 분리하는 선형분리를 찾는다. (최적의 decision boundary를 찾는다.)

좌측 2차원 좌표계에서 A=[a,d] ,B=[b,c]는 non-linearly separable(비선형 분리)하다.
이를 pi(x)를 통해 한 차원 높은 3차원으로 mapping하면 linearly separable(선형 분리)하게 할 수 있다.
충분히 큰 차원으로 적절한 비선형 매핑을 이용하면, 두 개의 클래스를 가진 이터 초평면(hyperplane)에서 항상 분리될 수 있다.
데이터가 선형으로 분리되어 있는 경우


위와 같이 분리할 수 있는 직선은 수없이 많이 존재한다.
SVM은 MMH(Maximum Marginal Hyperplane, 최대 마진 초평면)을 찾아 분리하는 방법이다.

분리 평면(Decision Boundary) 상에 있는 모든 값은 아래를 만족한다.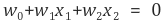
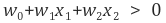

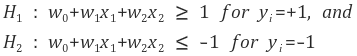 (서포터 벡터가 있는 영역의 w0+w1x1+w2x2 = +-1로 지정)
(서포터 벡터가 있는 영역의 w0+w1x1+w2x2 = +-1로 지정)
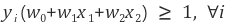 와 같이 쓸 수 있다.
와 같이 쓸 수 있다.
분리 평면 위에 있는 모든값,
분리 평면 아래에 있는 모든값,
따라서 가중치를 수정함으로서 마진(margin)의 면(side)를 정의하는 초평면을 다음과 같이 정의할 수 있다.
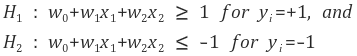 (서포터 벡터가 있는 영역의 w0+w1x1+w2x2 = +-1로 지정)
(서포터 벡터가 있는 영역의 w0+w1x1+w2x2 = +-1로 지정)위 두식을 결합하면,
서포터 벡터는 위의 등호가 성립하는 지점이다.

마진이 최대화 되는 식은 아래와 같이 변형 가능하다.
- - - - - 1
(최대 마진을 구하는 문제를 역수를 취함으로써, 최소화 하는 문제로 변형)
- - - - - 2
위 1, 2번 식을 만족하는 해를 찾아야 한다.
라그랑제 승수법를 통한 접근
각 조건식 마다 라그랑제 승수를 부여하여 라그랑제 함수 정의
KKT(Karush-Kuhn-Tucker)조건
1. 라그랑제 함수 에서 라그라제 승수를 제외한 로 편미분한 식이 이되어야 한다.
2. 모든 라그랑제 승수 은 0보다 크거나 같아야 한다.
따라서 모든 조건식에 대해 이거나 이 되어야 한다. 이때, 인 데이터 포인트가 바로 서포트 벡터이다